Critical Path Method (CPM) in Project Management: Explained

The critical path method (CPM) is a project scheduling algorithm used to calculate the total time needed to complete a project.

This makes it a great tool for any project manager to add to their arsenal. Best of all, once you learn the terminology and can look past the intimidating diagrams, you’ll find that CPM is surprisingly simple to use.

In this guide, we’ll teach you everything you need to know to use the critical path method, including:

• What the critical path is,
• How to calculate the critical path,
• What the benefits of CPM are, and
• How CPM is different from PERT and Gantt charts.

If you’re wholly new to CPM and don’t understand the associated technical terminology — like early start (ES) or total float (TF) — please refer to the CPM terminology section located at the end of this guide.

What is the critical path method (CPM)?

The critical path method is a scheduling algorithm that calculates how long a project will take to complete by identifying its critical path. 

The critical path is the longest sequence of dependent activities within a project. CPM also highlights how much extra time you have to perform activities that aren’t on the critical path, thereby showing you where you can be flexible without missing the deadline. 

This allows you to prioritize tasks and manage resources in a way that supports progress toward project completion.

How to find the critical path + example

Critical path method calculations are exceedingly simple — it’s just addition and subtraction, most commonly using days as the unit of measurement. 

Using the critical path method technique requires you to follow these 4 steps:

1. Create a Work Breakdown Structure,
2. Create a CPM diagram using task dependencies,
3. Do a forward pass to identify the critical path, and
4. Do a backward pass to calculate float.

So, let’s go through the critical path method step-by-step, using a YouTube video production project as an example.

Step #1: Create a Work Breakdown Structure

Step 1 of using the critical path method is creating a Work Breakdown Structure for your project.

Work Breakdown Structures are a complex subject in their own right, so we suggest reading our Work Breakdown Structure guide if you want to know more.

The short of it is this — a WBS is a hierarchical list of all tasks you’ll need to do to finish the project. 

Work Breakdown Structures are usually presented in the form of a tree diagram, but for the sake of CPM, you can just make a list.

You should also note down the duration of each task. Unfortunately, CPM doesn’t help you get this data, so it’s up to you how to decide on the duration for each task — estimates, guesstimates, previous experiences, etc.

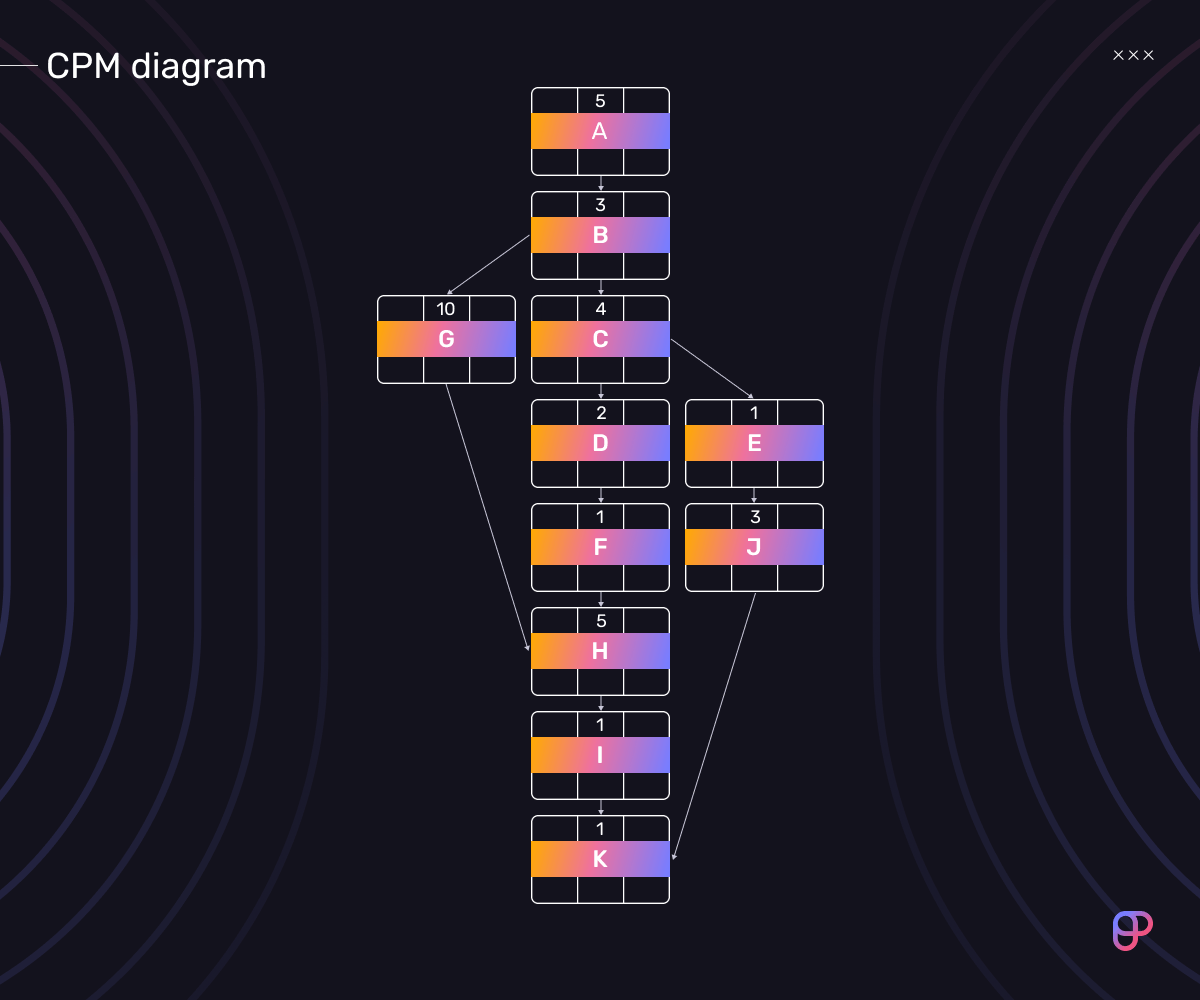
To make our YouTube video, we’ll need a simple WBS like this:

Task designation	Task description	Task duration
A.	Research the topic	5 days
B.	Create a concept	3 days
C.	Write a script	4 days
D.	Edit the script	2 days
E.	Create a title	1 day
F.	Record the voiceover audio	1 day
G.	Record the footage	10 days
H.	Edit the footage and audio	5 days
I.	Create thumbnails	1 day
J.	Promote the video on social media	3 days
K.	Upload the video to YouTube	1 day

Step #2: Create a CPM diagram

Step 2 of using the critical path method is drawing up a task diagram.

Once you’ve got the project task list and task durations ready, create an activity node for each activity.

To see how an activity node should look and what data goes where, refer to the terminology section at the end of this guide.

At this early stage, nodes will only contain their activity name and/or designation and duration:

• (c) Write a script, 3 days
• (g) Record the footage, 10 days

Connect the activity nodes with arrows to signify task dependencies. 

For example, editing a script is dependent on writing a script. The nodes will naturally branch out, but they will all converge to mark project completion.

With that done, you’ll be ready to start calculating the forward pass. 

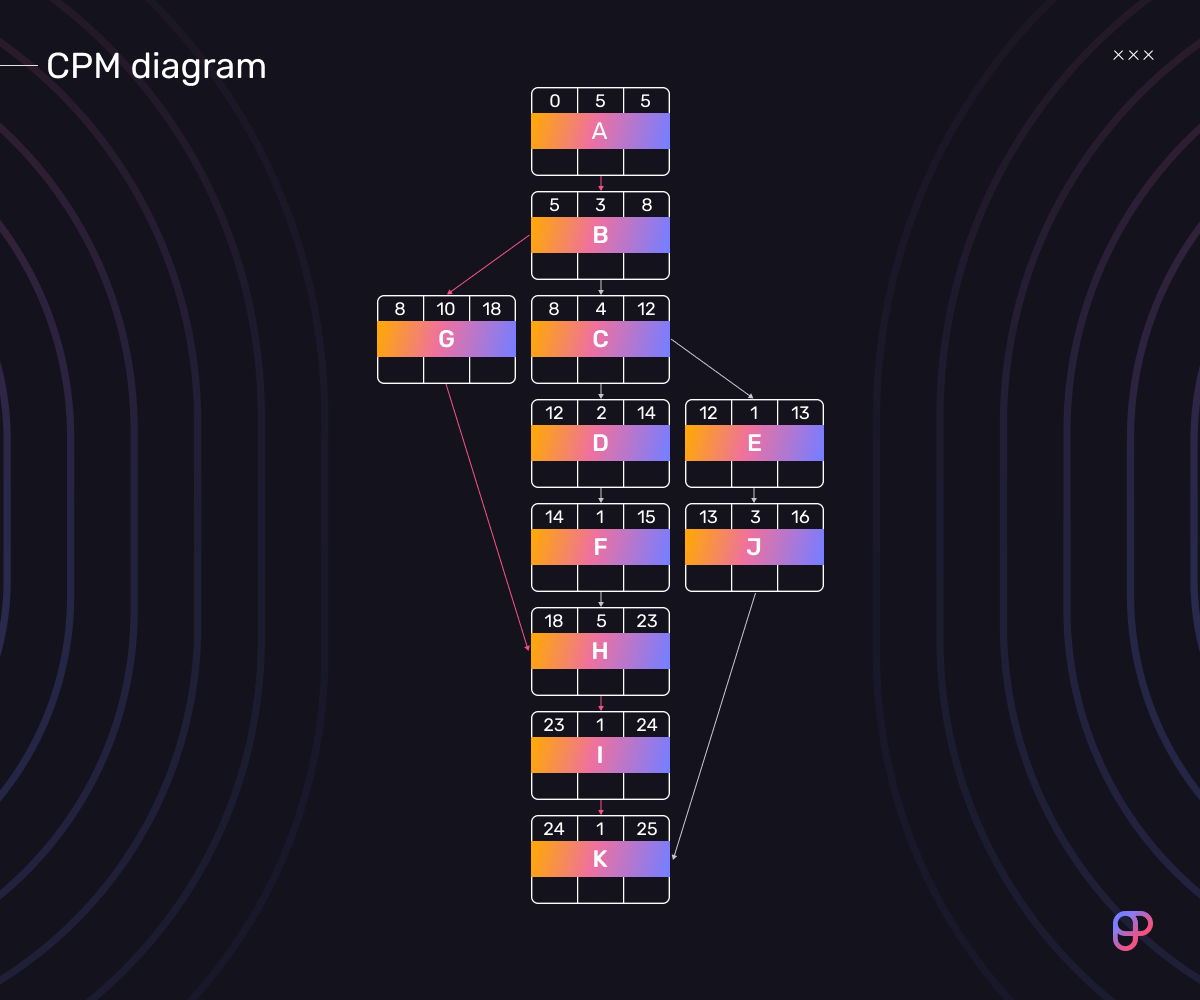
The image below shows what the CPM diagram of our project should look like at this point. We’ll fill in the blanks as we go through steps 3 and 4. 

Step #3: Do a forward pass

Step 3 of using the critical path method is doing a forward pass.

The forward pass is the act of calculating the early start (ES) and early finish (EF) times of all activities and highlighting the critical path. 

To calculate EF for each task, we will use the following formula: 

EF = ES + Dur

What keeps this formula simple is the fact that the starting activity always has an ES time of 0.

So, given that task (a) Research the topic has an ES of 0 and a duration of 5 days, its EF is 5.

EF = ES + Dur = 5 + 0 = 5

The EF of one activity is automatically assigned as the ES of all tasks immediately dependent on it. 

What this means is that the ES of task (b) Create a concept is 5 — the earliest you can start doing this task is on day 5. Since task (b) has a duration of 3 days, its EF is 8.

EF = ES + Dur = 5 + 3 = 8

Now, once you’ve finished work on task (b), you can immediately start working on two independent tasks — (c) Write a script and (g) Record the footage. Both of these tasks will have the same ES of 8, but different EF times.

EF = ES + Dur = 8 + 4 = 12

EF = ES + Dur = 8 + 10 = 18

Once you’ve done this for all activities, you can see which sequence of activities takes the longest to complete. 

Keep in mind that we are calculating the total time needed for project completion, not the number of activities.

In this example, the sequence of nodes that will take the longest to complete is (a)-(g)-(h)-(i)-(k) — this is the critical path. 

The sum total duration of this chain of activities is 25 days:

5 + 3 + 10 + 5 + 1 + 1 = 25

No matter what you do, you will not be able to complete the project in under 25 days, since that’s how much time all the tasks on the critical path require.

Step #4: Do a backward pass

Step 4 of using the critical path method is doing a backward pass.

Once we’ve finished calculating the forward pass to identify the critical path, it’s time to do a backward pass that’s used to calculate float.

Activities on the critical path don’t have float. 

If they get delayed or prolonged by even a day, the entire project gets delayed by the same amount. 

But, activities that aren’t on the critical path have some wiggle room.

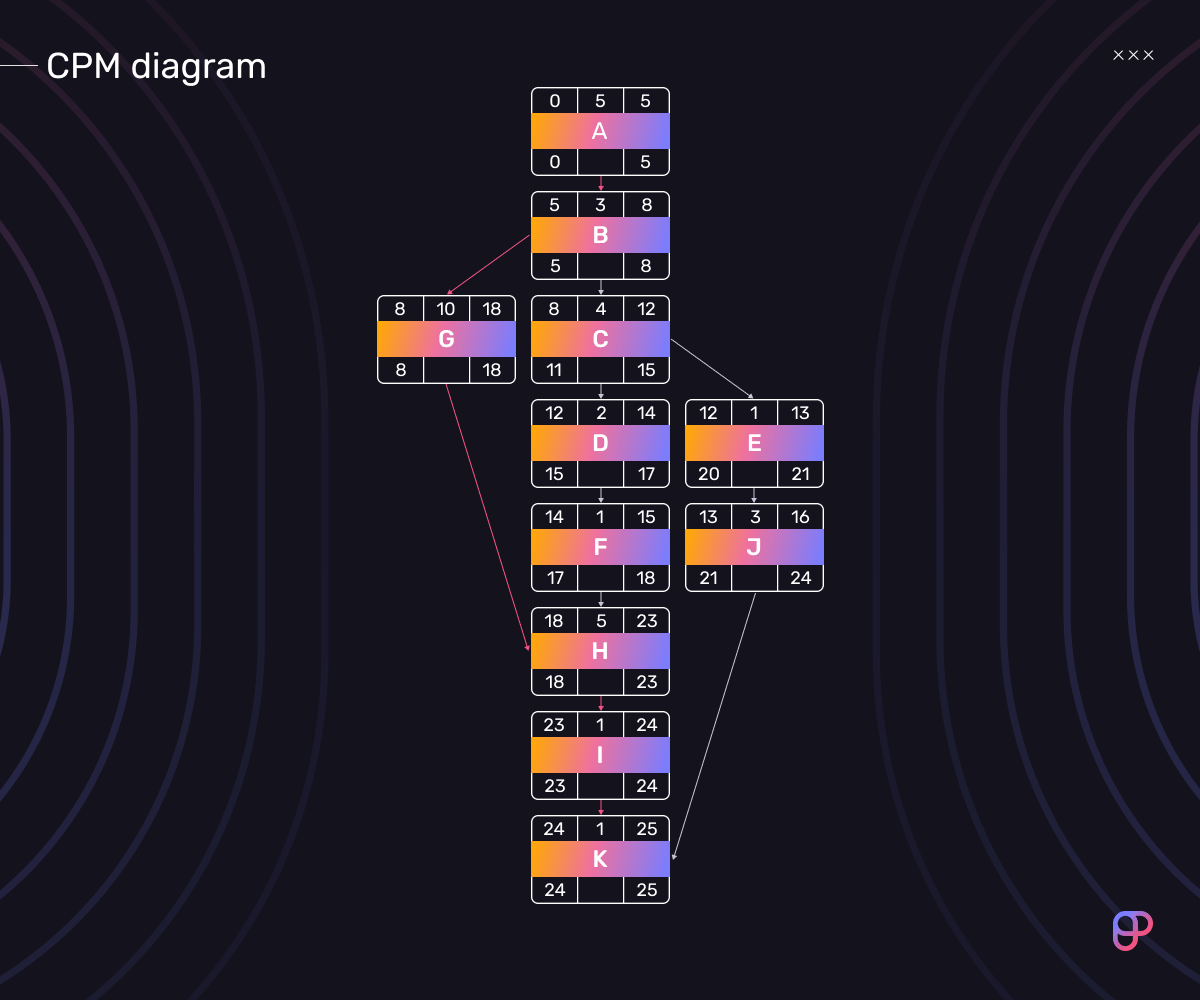
To calculate how much float other activities have, you’ll first need to calculate their late finish (LF) and late start (LS) times. 

The LF of a node is equal to the LS of the subsequent one. 

Activities on the critical path have equal values for their ES and LS, so we’ll take the final node as our starting point.

Therefore, node (j) Promote the video on social media has an LF of 24, as this is the LS value of node (k) Upload the video to YouTube. To calculate its LS, we use the following equation:

LS = LF – Dur = 24 – 3 = 21

We can then use the LS of task (j) to calculate the LF of (e) Create a title, and so on until we’ve done this for all tasks.

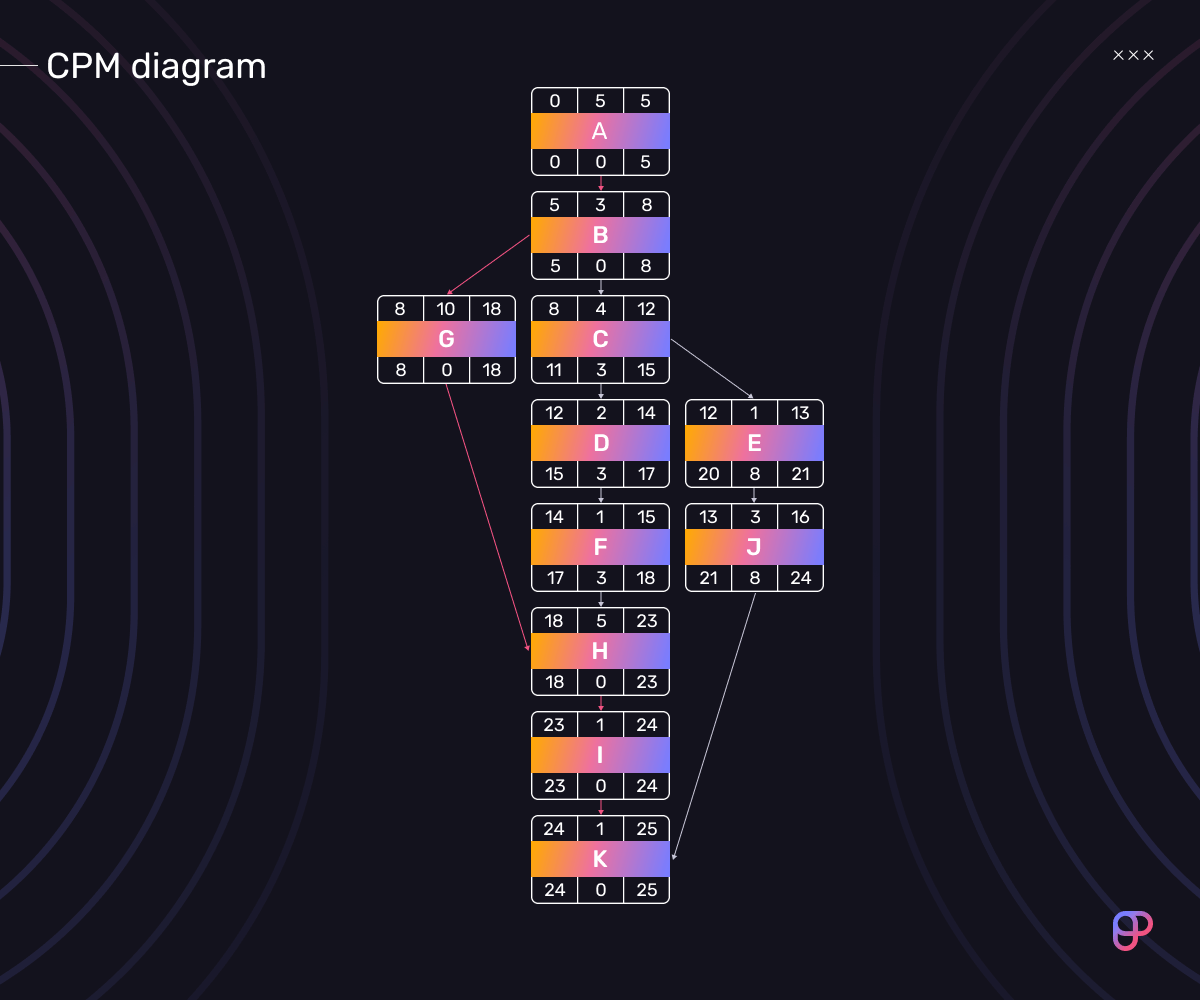
Now all that’s left to do is to calculate the float.

To do this, take any task and run it through either of these formulas:

TF = LF – EF 

TF = LS – ES 

Whichever formula you choose, you’ll get the same result. Let’s demonstrate this on task (j) Promote the video on social media:

TF = LF – EF = 24 – 16 = 8

TF = LS – ES = 21 – 13 = 8

What this shows us is that, even if promoting the video takes longer than expected, you won’t have any trouble since you have 8 days of breathing room to complete that task.

The CPM example — key takeaways

So, let’s walk through this example of the critical path method once more, this time without the math explainers.

We figured out which tasks need to be done to create a video from scratch and upload it to YouTube.

Then, we assigned a duration to each task and linked them for dependencies.

This is all the data we needed to do all the calculations necessary for using the critical path method.

The calculations showed us that the project would take at least 25 days to complete, and that’s if no tasks on the critical path get delayed.

It also showed us that work on the script and voiceover recording does not constitute a bottleneck in this project. The same goes for creating a title and promoting the video. 

Knowing that these tasks have float could help us distribute our efforts optimally. It would also enable us to divert some resources from tasks that have float to those that don’t and are struggling. 

For example, if the person capturing the footage needed help recording some segments, they could ask the scriptwriter for help without compromising the overall project progress. 

Why is the critical path method used?

The advantages of the critical path method are many, but we can divide them into 2 broad categories:

• Primary, and
• Secondary.

The primary advantages of the critical path method 

The first reason why you’d use the critical path method in project management is to calculate how long it will take to complete and create a schedule.

The other main advantage of the byproduct of creating the schedule and calculating the critical path leads to the other main advantages of the CPM project management technique — float. Namely, CPM shows you which project tasks can be extended without pushing back the project deadline.

Understanding float and using it to your advantage is where the real magic kicks in.

If and when a project encounters setbacks, the project manager can use float to formulate countermeasures that will bring the project back on track. 

For example, if a task that’s on the critical path is running late, they can divert resources from non-critical path tasks to speed it up. Even if this isn’t the ideal countermeasure, something has to be done because critical path tasks are the biggest progress bottlenecks in a project. 

On the other hand, if a task that’s not on the critical path is running late, they may not need to react in any way, provided the task has sufficient float. At the very least, they’ll know not to take resources away from tasks that are on the critical path — which would result in an even worse problem.

The secondary advantages of the critical path method

Another thing that CPM has going for it is that it’s easy to use. You just need to know what tasks need to be done, how they relate to one another, and how long each task will take. After that, it’s just a matter of simple addition and subtraction. 

Compared to input data used by other scheduling algorithms — like PERT, for example — this is as simple as it gets.

Lastly, CPM has a good track record. It was developed back in the 1950s by E.I. duPont de Nemours, a chemical company that had been suffering from production delays, and has been used ever since. 

The fact of the matter is that you don’t get to survive as a scheduling technique for over 70 years if you don’t give good results.

And, while the specifics of how to portray the CPM diagram have changed since then, the core of CPM has remained the same. 

In other words, it is still one of the best ways to map out a project schedule and increase its efficiency.

The disadvantages of CPM

Now, for all its benefits, CPM does carry some drawbacks that are worth pointing out.

First of all, CPM uses task duration as its primary input, but it doesn’t tell you how to estimate these durations. Meanwhile, any errors in these estimates can affect the calculations. This means that if your task duration assumptions are off, your calculations will be off as well.

Secondly, CPM assumes that time is the only constrained resource. Let’s refer back to the video production project example. If one person needs to do everything on their own, the critical path diagram is useless since one person can’t do 3 tasks at the same time.

What is the difference between the critical path method and other methodologies?

In case this wasn’t implicitly clear, we should explicitly state that the critical path method is not a project management methodology.

Therefore, comparing it to other project management methodologies or even Agile frameworks — like Waterfall, Kanban, or Scrum — would be equivalent to comparing ducks to duct tape.

Instead, it helps to think of CPM as one of the many project management tools within your arsenal. Just like you can use a task management platform like Plaky to keep track of progress and productivity, you can use CPM to chart out a project schedule. 

This also means you are free to use CPM regardless of which PM methodology you decide to follow, so long as the methodology in question doesn’t resist this kind of thorough preplanning. For example, Agile methodologies and CPM typically don’t mesh well because CPM requires you to have all project tasks mapped out from the get-go.

That being said, we certainly can compare the critical path method to other similar project management tools.

Given that CPM is a scheduling tool, the most immediate and most relevant comparisons can be drawn between it, PERT, and Gantt charts.

Critical path method vs PERT

PERT (Program Evaluation Review Technique) and CPM share a lot in common.

Not only are they both scheduling tools, but they were also developed around the same time.

Back when CPM was being developed at DuPont, the US Navy’s Polaris Project was also behind schedule.

PERT was the solution they developed to combat this issue.

Needless to say, it operated a bit differently.

Much like CPM, PERT requires you to break the project down into bite-sized tasks and map out the necessary sequence of tasks based on their dependencies. 

Unlike PERT, however, it provides some guidelines on how to estimate the duration of each task.

This is done by assigning each task 3 potential durations:

• The most optimistic (O) time needed to complete each task,
• The most probable (M) time needed to complete each task, and
• The most pessimistic (P) time needed to complete each task.

Once you have this data, you can calculate the PERT estimate (E) using the following equation:

E = (O + 4M + P) / 6  

In addition to this, charting out the timeline using PERT means starting from the deadline and working your way backward.

Critical path method vs Gantt chart

Gantt charts are bar charts used to visualize a project’s schedule.

Perhaps the most widely used scheduling tool today, Gantt charts were developed around the time of the First World War by Henry Gantt, who used them to measure the productivity of his employees. 

It didn’t take long for the US military to take notice of these charts and start implementing them in their operations.

Just like CPM, Gantt charts are used to visualize the flow of a project and link dependencies.

However, they don’t feature a system for calculating task durations.

In other words, once you already know how long each task will (or should) take, you can use Gantt charts to manage the project to great effect.

But you have to use another tool to calculate or estimate the task durations.

In this way, Gantt charts are compatible with CPM and PERT.

You can use the latter tools to map out the duration of a project with all its tasks and then use a Gantt chart to keep track of everything once the project gets underway. 

Doing this with CPM will also let you spot if the same person is assigned multiple tasks at the same time, thereby helping you avoid one drawback of using CPM.

Critical path method terminology

To those who have never used CPM, a critical path diagram will seem like some form of Elvish they can’t read.

But don’t let this dissuade you from using it. 

The truth of the matter is that the only math involved in CPM is simple addition and subtraction. Most projects also measure task duration in days, removing the need to fiddle with hours and minutes.

In other words, the math required for calculating the critical path method couldn’t be simpler.

But to do these calculations, you first need to get acquainted with CPM’s acronym-heavy terminology. 

So, let’s quickly explain the following CPM terms:

• Critical path,
• Activity nodes,
• Early start time (ES),
• Early finish time (EF),
• Late finish time (LS),
• Late start time (LF),
• Total float/slack (TF), and
• Free float (FF).

Term #1: Critical path

The critical path is the sequence of dependent activities with the longest overall duration.

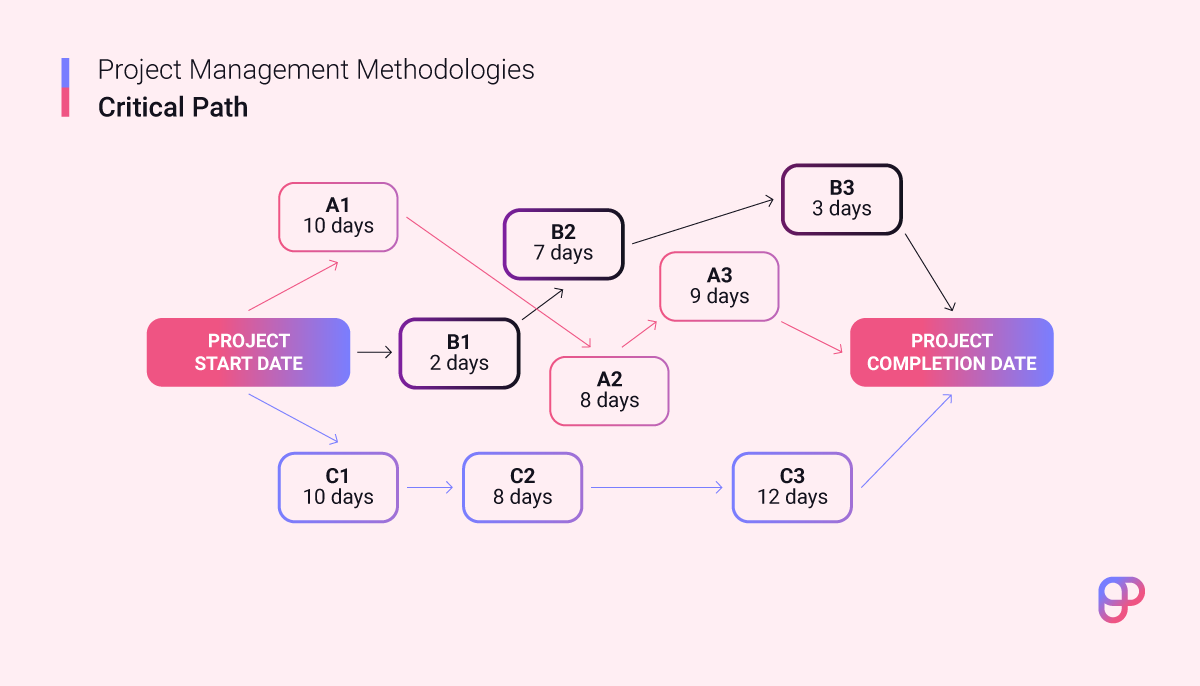
In the diagram above, the C1-C2-C3 string of activities constitutes the critical path, as they take 30 days to complete.

The alternative routes — consisting of activities A1-A2-A3 OR B1-B2-B3 — take only 27 days and 12 days to complete respectively. 

In other words, no matter how quickly you go through these secondary routes, the project won’t be completed until the activities on the critical path get done. Even if activities B1, B2, and B3 took twice as long to complete, they wouldn’t impact the deadline at all.

Term #2: Activity nodes

Activity nodes are rectangles used in CPM diagrams designed to hold all the crucial information needed for charting a project’s critical path.

Once upon a time, CPM was performed using the so-called activity-on-arrow diagrams. These diagrams contained much of the same information but were more visually confusing.

Nowadays, activity-on-node diagrams are more popular. As the more intuitive method, this is the only type of diagram we’ve used in this guide.

Each task required for project completion gets its own activity node. The illustration above features 9 activity nodes: A1, A2, A3, B1, B2, B3, C1, C2, and C3. 

These nodes are then linked with arrows to point out task dependencies — you can’t begin work on A2 before you’ve completed task A1.

In addition to the activity name, the node also contains all the following data found in the picture below.

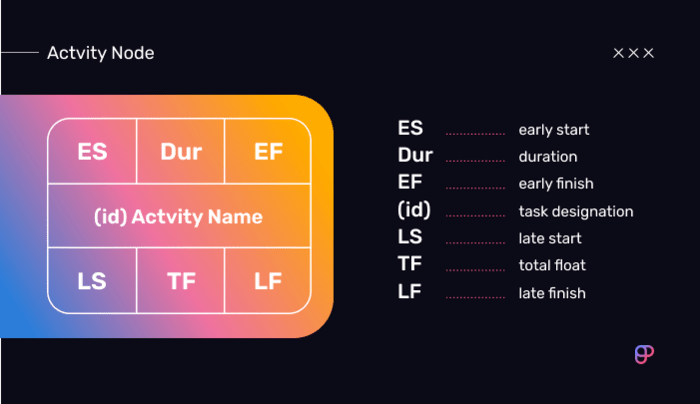
Term #3: Early start time (ES)

Early start time denotes the earliest possible point at which you can start working on a task. 

The ES for the first task(s) in a project is set to 0. 

To calculate the ES for all other tasks, just copy the EF (early finish time) of the preceding dependent task. If a task is dependent on 2 or more previous activities, refer to the activity with the longer ES.

In case this sounds confusing, let’s apply the principle to the simplest activity imaginable — making tea. 

You want to make a cup of tea, but all your teacups are dirty. 

Making tea depends on 2 tasks — boiling water and washing a teacup. 

The water takes 5 minutes to boil, but you can wash a cup in 30 seconds. You can do these activities at the same time, but the earliest time at which you’ll be able to make tea corresponds to when you finish the longer of the dependent tasks. 

In this example, making tea has an ES of 5 minutes — because this is the time of the longer of the dependent tasks.

Term #4: Duration (Dur)

Duration is self-explanatory — it denotes how long you expect a task will take to complete.

Term #5: Early finish time (EF)

Early finish time denotes the earliest moment at which it is possible to finish a task. 

To calculate the early finish time for a task, you take its ES and add the task duration (Dur).

EF = ES + Dur

Since the first activity in a project generally has an ES of 0, the EF will be identical to the duration of the first activity.

All dependent tasks that follow immediately after it will take the first task’s EF as their ES, and add their duration to it to calculate their EF.

Term #6: Late finish time (LF)

Late finish time denotes the latest point at which you can complete an activity without it prolonging the overall project timeline.

Tasks that are on the critical path have identical LF and EF values. 

To calculate the LF of tasks that aren’t on the critical path, you have to start with the project completion node and work your way backward. The LF of a node is equal to the LS (late start time) of its subsequent dependent node. 

This is another equation that looks way more complicated in isolation, so let’s simplify it using the previous tea-making example. 

The final activity (making the tea) has an LS of 5 minutes. This is the LF value of all activities that lead into it. So, both washing the cup and boiling the water have an LF value of 5 minutes.

Term #7: Late start time (LS)

Late start time denotes the latest point at which you can start work on an activity without having it prolong the overall project timeline.

To calculate the LS of an activity, use the following formula:

LS = LF – Dur 

In our example, washing the cup takes 30 seconds. This activity has an LF of 5 minutes. Therefore, its LS equals 4 minutes and 30 seconds. 

In other words, if you start washing the cup at the 4-minute and 30-second mark, you’ll still be able to start making tea on schedule. 

Any later than that, and your boiling water will be waiting for you to finish washing the teacup, thereby extending your afternoon-tea timeline.

Term #8: Total float/slack (TF)

Total float and total slack denote the amount of wiggle room you have before you must start working on tasks that are not on the critical path.

Float and slack are synonymous, the only difference between the two lies in your attitude — float is how much extra time you can dedicate to tasks whereas slack is how long you can procrastinate.

They’re even calculated using the same formula. 

To calculate total float/slack, use either of the following formulas:

TF = LF – EF

TF = LS – ES

In the tea-making example, boiling the water has no float since it’s on the critical path.

Washing the cup has a total float of 4 minutes and 30 seconds.

Term #9: Free float (FF)

Free float is the same as total float — it even uses the same formula. 

The difference between them is entirely contextual. 

When we have several non-critical path tasks chained together, the backward pass calculations show that they all have the same float. 

But if you extend one of those tasks by any amount, you’ll reduce the remaining float of subsequent tasks in that chain. 

However, you’ll sometimes run into non-critical path tasks that aren’t part of an expanded chain of non-critical path tasks. We say that those tasks have free float because using up their float won’t reduce the float of any subsequent activity.

For example, if we had just one task labeled A instead of the task chain A1-A2-A3, then A would have free float.

📖 Now that you understand how the Critical Path Method works, dive further into the subject of project management — explore our Project Management Glossary of Terms.

Use the right tool for the job — try Plaky for free

The critical path method is a superb tool for project planning, but things rarely go according to plan. To ensure your project stays on schedule, you need to be able to track progress accurately and adapt to changing situations.

This is where specialized project management software such as Plaky comes in. Among other things, Plaky allows you to:

• Have all your project and task information in one place,
• Use Gantt charts to visualize the schedule and adapt to changes easily,
• Have insight into all project activities,
• Automatically calculate costs, 
• Set projects up using versatile project templates, and more.

If you’d like to try out the app for yourself, you can create a free Plaky account today and test out the full feature set for 14 days — no strings attached!

References

• Accettura, A., Bergsma, K., Boszak, T., Callaway, J. L., Cote, N., Doepker, C. Harbidge, M., Her, S., Hlushko, T., Holmes, J., Knight, M., MacDowell,  P., Marshall, C., McDougall, L., Prima, A., & Story, T. (2021). Project Management for Instructional Designers, First Canadian Edition. Retrieved from http://pm4id.ca. Licensed under a Creative Commons Attribution NonCommercial ShareAlike (BY-NC-SA) license.
• Arun, R. (2021, October 14). Everything You Need To Know About CPM: The Critical Path Method. https://www.simplilearn.com/tutorials/project-management-tutorial/critical-path-method
• Kent, R. (2017). Quality Management in Plastics Processing. William Andrew Publishing. https://www.sciencedirect.com/topics/engineering/arrow-diagram
• Levy, F. K., Thompson, L. G., & Wiest, J. D. (1963). The ABCs of the Critical Path Method. Harvard Business Review. https://hbr.org/1963/09/the-abcs-of-the-critical-path-method
• Wallace, C. (2017, December 31). This Project Management Technique Is More Than A Productivity Hack. Forbes. https://www.forbes.com/sites/christinawallace/2017/12/31/no-more-productivity-hacks-2018/